Loew Hall 113
Factoring cycles
Victor Reiner from University of Minnesota
A classic result of Hurwitz, often credited to Dénes, says that in the symmetric group on n letters, there are nn-2 ways to factor an n-cycle into n-1 transpositions. Recent joint work with J. Lewis and D. Stanton (arXiv:1308.1468) uncovered a finite field q-analogue: in the general linear group GLn (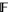
q), there are (qn-1)n-1 ways to factor a Singer cycle into n reflections.
This talk will discuss what this means, and how to prove such things.