A Proof of Grünbaum's Lower Bound Conjecture for general polytopes, and strongly regular CW spheres

Lei Xue, University of Washington

Wednesday, February 17 2021, 3:30 - 5pm

via Zoom

$Lei Xue$

Note: This talk begins with a pre-seminar (aimed at graduate students) at 3:30–4:00. The main talk starts at 4:10.

Join Zoom Meeting: https://washington.zoom.us/j/91547335974
Meeting ID: 915 4733 5974

In 1967, Grünbaum conjectured that any 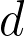$d$ -dimensional polytope with 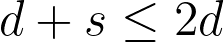$d+s\leq 2d$ vertices has at least

$\phi_k(d+s,d) = {d+1 \choose k+1 }+{d \choose k+1 }-{d+1-s \choose k+1 }$

$k$ -faces. In the talk, we will discuss the proof of this conjecture and also characterize the cases in which equality holds. Our results extend to strongly regular CW spheres. We will also talk about recent results on $d$ -dimensional polytope with $2d+1$ or $2d+2$ vertices.

Event Type

Seminars

Event Subcalendar

Combinatorics and Geometry Seminar